Fisher–Tippett–Gnedenko theorem

In statistics, the Fisher–Tippett–Gnedenko theorem (also the Fisher–Tippett theorem or the extreme value theorem) is a general result in extreme value theory regarding asymptotic distribution of extreme order statistics. The maximum of a sample of iid random variables after proper renormalization converges in distribution to one of 3 possible distributions, the Gumbel distribution, the Fréchet distribution, or the Weibull distribution. Credit for the extreme value theorem (or convergence to types theorem) is given to Gnedenko (1948), previous versions were stated by Fisher and Tippett in 1928 and Fréchet in 1927.

The role of extremal types theorem for maxima is similar to that of central limit theorem for averages.

Statement

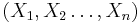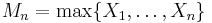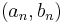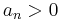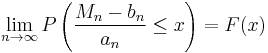Let $(X_1,X_2\ldots, X_n)$ be a sequence of independent and identically-distributed random variables, let $M_n=\max\{X_1,\ldots,X_n\}$ . If a sequence of pairs of real numbers $(a_n, b_n)$ exists such that each $a_n>0$ and: $\lim_{n \to \infty}P\left(\frac{M_n-b_n}{a_n}\leq x\right) = F(x)$ then if $F$ is a non degenerate distribution function, it belongs to either the Gumbel, the Fréchet or the Weibull family. These distributions are particular cases of more general extreme value distribution.

Conditions of convergence

If G is the distribution function of X, then M_n can be rescaled to converge in law to

a Fréchet iff G < 1 and $\frac{1-G(tx)}{1-G(t)}\xrightarrow[t\to %2B\infty]{} x^{-\theta}, \quad x>0$ . In this case we can take b_n = 0 and 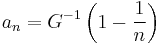$a_n=G^{-1}\left(1-\frac{1}{n}\right)$ .
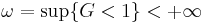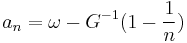a Weibull iff $\omega = \sup\{G<1\} <%2B\infty$ and $\frac{1-G(\omega%2Btx)}{1-G(\omega-t)}\xrightarrow[t\to 0^%2B]{} (-x)^\theta, \quad x<0$ . In this case we can take b_n = ω and $a_n=\omega - G^{-1}(1-\frac{1}{n})$ .

Fisher–Tippett–Gnedenko theorem

Statement

Conditions of convergence

See also